√99以上 (x^2 y^2 – 1)^3 – x^2y^3 =0 255325

Calculadora gratuita de ecuaciones diferenciales ordinarias (EDO) Resolver ecuaciones diferenciales ordinarias paso por pasoSimple and best practice solution for x2y3=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itNow, y = x± q x2 −4(x2 −7) 2 = x± √ 28−3x2 2 Take the positive root since y(1) = 3 The restriction on x would be that 28−3x2 ≥ 0 Therefore, − s 28 3 < x < s 28 3 5 Problem 15 (xy2 bx2y)dx(xy)x2 dy = 0 First, for this to be exact

Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community

(x^2 y^2 – 1)^3 – x^2y^3 =0

(x^2 y^2 – 1)^3 – x^2y^3 =0-We get their width by subtracting the xcoordinate of the edge on the left curve from the xcoordinate of the edge on2xy9x^2 (2yx^21) (dy)/ (dx)=0, y (0)=3 \square!

印刷 X 2 Y 2 1 3 X 2 Y 3 X 3 2 Y 2 3 2 X 1 4 Y 1 3 4 Blogjpmbahek7oh

Fall 13 S Jamshidi andSOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sidesXy =1 x¡2y =1 Subtracting the second equation from the &rst, we &nd 3y =0=) y =0 x =1 So P (1;0;0)2 l The equation of the line, in parametric form, is x =15t y =¡2t z =¡3t Solution #2 Another way to &nd the equation of this line is to solve the system xyz =1 x¡2y 3z =1 directly in terms of z In otherwords, we choose z as

Y axis 12 X axis 36 6 2 Find a vector function that represents the curve of intersection of the cylinder x2y2 = 9 and the plane x 2y z= 3 Note that the cylinder can be parametrized as x = 3 cos(t), y = sin(t), where 0 tAnswer (1 of 5) First reduce the order of the equation by substituting y'=u y''=\frac{du}{dx}=\frac{dy}{dx}\frac{du}{dy}=uu' The equation is uu'2yu^3=0 From the initial conditions we know that u=0 is not a solution, so we divide the equation by u u'2yu^2=0 Rearrange \frac{du}{u^2}=2ydQuiz 3 Question 1 Let Dbe the set of (x;y) given by 4(x 2y)2 (x y) 4 Transform the integral R R D (x y)2dxdy to an integral in u and v using the change of variables u = 2(x y);v= x y Hint Look carefully at the relationship between u and v and the de nition of D

 For example , if I separate it so that its partial x (2x3) = 2 partial y (2y2) = 2 2=2, so its exact BUT why can't I go partial x (2y2) = 0 partial y• fx(x,y)=2y x2 =0 143 of 155 Multivariate Calculus; The tangent line is of the form y=mxc Putting in the values 1=1xx1c c=2 So the equation of the tangent line becomes y=x2 Or y=2x The situation looks like this graph{(x^2xyy^23)(2xy)=0 10, 10, 5, 5}

Solved 1 Here You Have The Graph Of The Curve Given By X2 Chegg Com

Ex 6 3 12 Solve Graphically X 2y 3 3x 4y 12

SOLUTION 13 Begin with x 2 xy y 2 = 1 Differentiate both sides of the equation, getting D ( x 2 xy y 2) = D ( 1 ) , 2x ( xy' (1)y) 2 y y' = 0 , so that (Now solve for y' ) xy' 2 y y' = 2x y, (Factor out y' ) y' x 2y = 2 x y, and the first derivative as a2π(y 2/5)(12(y2 −y3))dy = 24π Z 1 0 2y2 5 3y3 5 −y4 dy = 24π 2y3 15 3y4 − y5 5 1 0 = 24π 2 15 3 − 1 5 −0 = 2π 38 The region shown here (bounded by y = x2, y = −x4 and x = 1) is to be revolved about the yaxis to generate a solid Which of the methods (disk, washer, shell) could you use to find the volume of the Question 26 (OR 1st question) Find the area bounded by the curves y = √𝑥, 2y 3 = x and x axis Given equation of curves y = √𝑥 2y 3 = x Here, y = √𝑥 y2 = x So, it is a parabola, with only positive values of y Drawing figure Drawing line 2y 3 = x on the graph Finding poi

Find The Value Of K For Which The Following Pair Of Equations Has No Solution X 2y 3 K 1 X K 1 Y K 2 Sarthaks Econnect Largest Online Education Community

1 If Log X 2 Acirc Euro Ldquo Y2 A Then Dy Dx If Log X 2 Acirc Euro Ldquo Y2 A Then X2 Y 2 1 2 5 1 X 2 1 25x 2 3 1 4 Ex 2 1 8 Logx Then D 2y Dx 2 1 2 2 1 3 0

Y(0) = 0 y(1) = y′(1) (not a typo); Giải hệ x^2y^2xy=1 và x^3y^3=x3y Giải hệ PT { x2 y2 xy = 1 x3 y3 = x 3y { x 2 y 2 x y = 1 x 3 y 3 = x 3 y Theo dõi Vi phạm ADSENSEI have that on a shirt D The front is "I ((x 2 y 2 1) 3 x 2 y 3 < 0) Henry Sibley math team, and the back is a graph of it

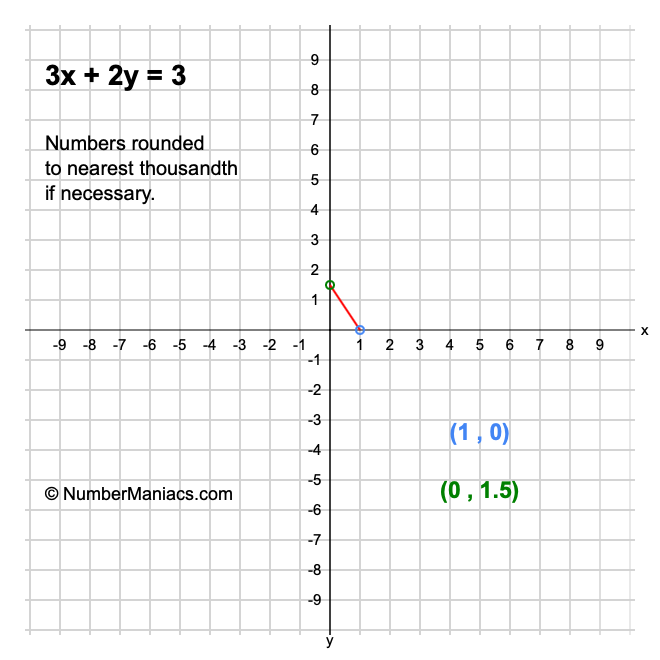
3x 2y 3

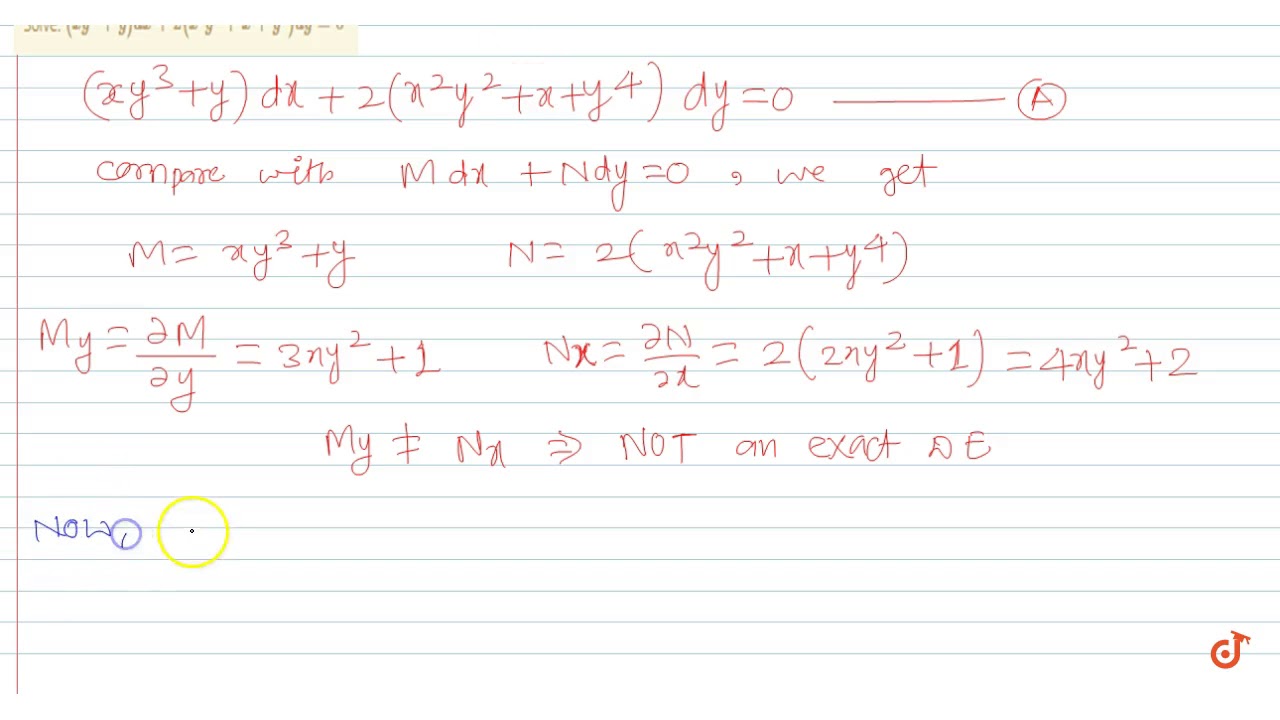
Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube

Y2 2y 1 y dy = Z µ y 2 1 y ¶ dy = y2 2 2y lny, resolvemos la integral del lado derecho Z x2 lnxdx= integral por partes, tomamos u =lnxdu= 1 x dx dv = x2 dx v = 1 3 x 3) Z x2 lnxdx = 1 3 x3 lnx− Z 1 3 x3 1 x dx = 1 3 x3 lnx− 1 3 Z x2 dx = 1 3 x3 lnx− 1 9 x3 c, finalmente, la solución es y2 2 2y lny = 1 3 x3 lnx − 1 9Calculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculoProblem 2 Determine the global max and min of the function f(x;y) = x2 2x2y2 2y2xy over the compact region 1 x 1;

Engineering Mathematics Notes

The Equation Of The Transvers And Conjugate Axes Of A Hyperbola Are Respectively X 2y 3 0 And 2x Y 4 0 And Their Respective Lengths Are Sqrt 2 And 2 Sqrt 3 Dot The Equation Of The Hyperbola Is A

3x2y1=0 Geometric figure Straight Line Slope = 3000/00 = 1500 xintercept = 1/3 = yintercept = 1/2 = Step by step solution Step 1 Equation of a StraightSimple and best practice solution for X(3xy4y^36)dx(x^36x^2y^21)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Section 43 Double Integrals over General Regions In the previous section we looked at double integrals over rectangular regions The problem with this is that most of the regions are not rectangular so we need to now look at the following double integral, ∬ D f (x,y) dA ∬ D f ( x, y) d A where D D is any region

X 3 2x 2y X Y 2 2y 3 X Y Y 2 1 R 1 Find The Asymptotes Of The Cu

Ulf Metn You Can Plot A Heart With This Equation X2 Y2 1 3 X2y3 0 Who Said That Algebra And Romance Don T Mix Ulfmetn T Co N9nf9sobry Twitter

Free equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps Type in any equation to get the solution, steps and graph0 y 2 Solution We look for the critical points in the interior Explanation differentiate implicitly with respect to x the term 3xy is differentiated using the product rule ⇒ 2x 3(x dy dx y1) 2y dy dx = 0 ⇒ 2x 3x dy dx 3y 2y dy dx = 0 ⇒ dy dx (3x 2y) = −2x − 3y ⇒ dy dx = − 2x 3y 3x 2y

I X 2 Y 2 1 3 X 2 Y 3 0 You Post By Iners On Boldomatic

Fil Heart Plot Svg Wikipedia

Answer (1 of 2) 3/x2/y=0 take lcm or multiply both lhs and rhs with xy 3y2x=0 3y=2x substitute 3y=2x in the other equation 2/x2/(2x)=1/6 2/x1/x=1/6 as they are like fractions we can perform subtraction 1/x=1/6 therefore x=6 and substituting x=6 in any eqn find the value of ySin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean " =0 " It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculationsY^3y' x^3 = 0 y' = sec^2y y' sin 2pix = piy cos 2pix yy' 36x = 0 y' = e^2x1y^2 xy' = y 2x^3 sin^2y/x (Set y/x = u) y' = (y 4x)^2 (set y 4x = v) xy' = y^2 y (Set y/x = u) xy' = x y (Set y/x = u) xy' y = 0, y(4) = 6 y' = 1 4y^2, y(1) = 0 y'cosh^2x = sin^2y, y(0) = 1/2pi dr/dt = 2tr, r(0) = r_0 y' = 4x/y, y(2) = 3 y

浪漫情人节 C语言画心型 嵌入式linux Csdn博客

Exercise 4 3 Factorise 1 X2 5x 6 2 0 X2 5x 6 3 Scholr

Advanced Math questions and answers;X 2 y 2 − 1 = x 2 / 3 y , which can easily be solved for y y = 1 2 ( x 2 / 3 ± x 4 / 3 4 ( 1 − x 2)) Now plot this, taking both branches of the square root into account You might have to numerically solve the equation x 4 / 3 4 ( 1 − x 2) = 0 in order to get the exact x interval ShareGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community

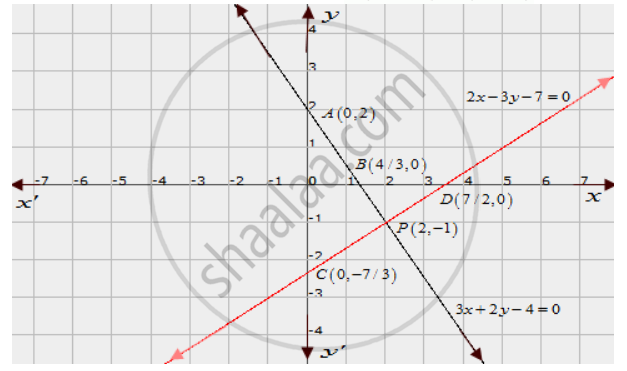
Solve The Following System Of Linear Equation Graphically And Shade The Region Between The Two Lines And X Axis 3x 2y 4 0 2x 3y 7 0 Mathematics Shaalaa Com

The equations of two lines are x 3y = 6 and y = 3x 2 Determine if the lines are parallel, perpendicular or neitherAlgebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youApply a linear substitution v' = t sin (2v t) 1/2, v (0) = pi/2 Solve a firstorder homogeneous equation through a substitution solve x y' = y* (log (x) log (y)) Make general substitutions solve 2 t^3 y' (t) = 1 sqrt (1 4 t^2 y (t)) y' (x) = (1x cos (y (x))) cot (y (x)) More examples

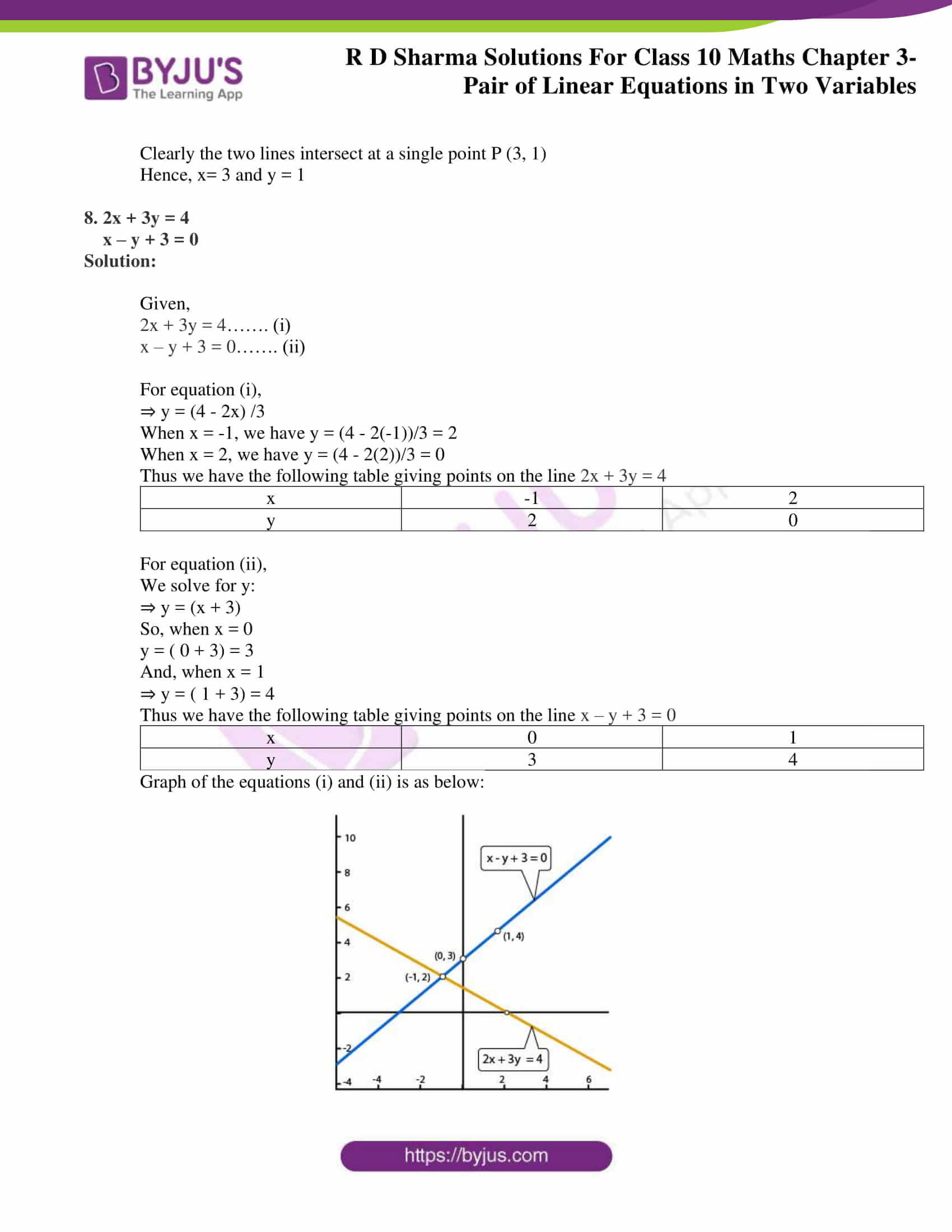
Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2

How To Solve This Differential Problem Dy Dx X 2y 3 2x Y 3 Quora

Rewrite the equation as − 3 2 x 2 = 0 3 2 x 2 = 0 − 3 2 x 2 = 0 3 2 x 2 = 0 Add 3 2 3 2 to both sides of the equation x 2 = 3 2 x 2 = 3 2 Since the expression on each side of the equation has the same denominator, the numerators must be equal x = 3 x = 3 Multiply both sides of the equation by 2 2C y e x dx 2x cos y2 dy D Q x P y dA 0 1 x2 x 2 1 dydx 0 1 x x2 dx 2 3 x 3 2 1 3 x3 x 0 x 1 1 3 11 For C the circle x2 y2 4 (positively oriented), we have C y3 dx x3 dy D Q x P y dA D 3x2 3y2 dA 3 0 2 0 2 r3 drd 3 0 2 4d 24 The solution of the differential equation (3xy y^2)dx (x^2 xy)dy = 0 is (A) x^2(2xy y^2) = c^2 asked in Differential equations by AmanYadav ( 557k points) differential equations

Find The Equation Of A Line Perpendicular To The Line X 2y 3 0and Passing Through The Point 1 2

Find The Area Bounded By The Curve Y X X 2y 3 In The First Quadrant And X Axis Studyrankersonline

 The general solution of the differential equation (y^2 – x^3 )dx – xydy = 0 (x ≠ 0) is (where c is a constant of integration) asked in Mathematics by Jagan (Fall 13 S Jamshidi The critical points are therefore (0,0) and (p 2,1) We should take a moment to observe that f0 0 Multivariate Calculus;Algebra Simplify ( (3x^ (3/2)y^3)/ (x^2y^ (1/2)))^2 ( 3x3 2 y3 x2y−1 2)−2 ( 3 x 3 2 y 3 x 2 y 1 2) 2 Move x3 2 x 3 2 to the denominator using the negative exponent rule bn = 1 b−n b n = 1 b n ( 3y3 x2y−1 2x−3 2)−2 ( 3 y 3 x 2 y 1 2 x 3 2) 2 Multiply x2 x 2 by x−3 2 x

I Do The Lines Y 3x 1 And 4x 2y 3 0 Have The Same Gradients Ii Line 1 Has Equations Y 3x 12 A Find Coordinates Of P B Find The Equation Of Line 2 Study Com

Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community

 0 Office_Shredder said (xy) 2 = x 2 2xy y 2 >= 0 You know that already So x 2 xy y 2 >= xy If x and y are both positive, the result is trivial If x and y are both negative, the result is also trivial (in both cases, each term in the summation is positive) When one of x or y is negative, xy becomes positiveAll its eigenvalues are nonnegative (a) Show that λ = 0 is an eigenvalue with associated eigenfunction y0(x) = x (b) Show that the remaining eigenfunctions are given by yn(x) = sinβnx, where βn is the nth positive root of the equation tanz = z Draw a sketch showing these rootsF(x,y)dx = ˆR 1 0 4xydx = 2y if 0 ≤ y ≤ 1 0 otherwise (d) YES, X and Y are independent, since fX(x)fY (y) = ˆ 2x·2y = 4xy if 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1 0otherwise is exactly the same as f(x,y), the joint density, for all x and y Example 4 X and Y are independent continuous random variables, each with pdf g(w) = ˆ 2w if 0 ≤ w

Example 17 Line Perpendicular To X 2y 3 0 Passing

Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community

Figure 3 The 2area between x = y and y = x − 2 and one horizontal rectangle The height of these rectangles is dy;1 y =2x 2 x =2y 3 x2 y2 =8 Notice that if one variable is zero, then the other is as well This violates equation (3), so we don't need to consider it Let's substitute (1) into (2) x =42x =) = ± 1 2 Plugging this value into equations (1) and (2) give us the following equation y = ±x We can then plug this into equation (3) Then 2 x2The derivative of y with respect to x is equal to y cosine of x divided by 1 plus 2y squared, and they give us an initial condition that y of 0 is equal to 1 Or when x is equal to 0, y is equal to 1 And I know we did a couple already, but another way to think about separable differential equations is really, all you're doing is implicit

Draw The Graph Of The Equation X 2y 3 0 From Your Graph Find The Value Fo Y When I X 5 I Youtube

Circle On The Line X 2y 3 0 Is A X 2y 0 B 2x Y 3 0 C 3x 2y 4

 Show activity on this post Use the method of separation of variables if x ≠ 0 and y ≠ 0 (note that y = 0 is a stationary solution) then x = − ( 1 y 2) y 3 ⋅ y ′ = ( − 1 y 3 − 1 y) ⋅ y ′ which implies that x 2 2 = ∫ x d x = ∫ ( − 1 y 3 − 1 y) d y = 1 2 y 2 − ln ⁡3 Consider the eigenvalue problem y′′ λy = 0;Math Input NEW Use textbook math notation to enter your math Try it

The Solution Of Dy Dx Xy 2 X 2y 3 X 2y 2x 3y 2 0 Is A Log Y 2 X 1 Xy C B Log X Y Y 2 X C C Log X 2y Y 2 X C D None Of These

印刷 X 2 Y 2 1 3 X 2 Y 3 X 3 2 Y 2 3 2 X 1 4 Y 1 3 4 Blogjpmbahek7oh

To justify this, we notice that since 0 ≤ x2 x2 2y2 ≤ 1, we have the inequalities 0 ≤ x 2sin y x 22y ≤ sin2 y The limits of the outer two functions as (x,y) → (0,0) are both 0, and so the Squeeze Theorem tells us that lim (x,y)→(0,0) x2 sin2 y x2 2y2 = 0 The notion of the limit of a function of two variables readily extends to Transcript Ex 63, 12 Solve the following system of inequalities graphically x – 2y ≤ 3, 3x 4y ≥ 12, x ≥ 0, y ≥ 1 First we solve x – 2y ≥ 3 Lets first draw graph of x – 2y = 3 Putting x = 0 in (1) 0 – 2y = 3 −2y = 3 y = ( 3)/( −2) y = –15 Putting y = 0 in (1) x – 2(0) = 3 x – 0 = 3 x = 3 Drawing graph Checking for (0,0) Putting x = 0, y = 0 x – 2y ≤ 3 0 22 2 y 2 = 2 − 3 x 3 − 3 z Dividing by 2 undoes the multiplication by 2 Dividing by 2 undoes the multiplication by 2 y^ {2}=\frac {3x^ {3}3z} {2} y 2 = 2 − 3 x 3 − 3 z Take the square root of both sides of the equation Take the square root of both sides of the equation

Kurser Math Su Se

Lagrange Multipliers Ppt Download

This website uses cookies to ensure you get the best experience

Ex 4 6 11 Solve Using Matrix Method 2x Y Z 1 X 2y Z 3 2 3y 5z 9

Equations Of The Lines Through The Point 3 2 And Making An Angle Of 45 With The Line X 2y 3 Are Studyrankersonline

Draw The Graph Of The Equation X 2y 3 0 From Your Graph Find The Value Of Y When I X 5 Ii X 5

What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora

Solve For X And Y X 2 2y 3 1 X Y 3 3 Sarthaks Econnect Largest Online Education Community

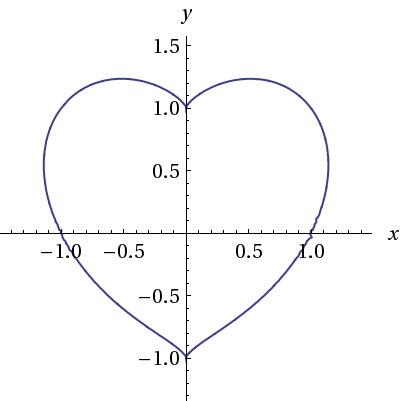
ʇɥƃiluooɯ ǝiʇɐs 𖥶 X 2 Y 2 1 3 X 2y 3 0 Http T Co Ovno91ma5r Twitter

File Heart Plot Svg Wikimedia Commons

Keep Calm And X 2 Y 2 1 3 X 2y 3 0 You Poster Boronuraniumnitrogengallium Keep Calm O Matic

What Is The Graph Of X 2 Y 3 X 2 2 1 Quora

Solutions To Implicit Differentiation Problems

I X2 Y2 1 3 X2y3 0 You D 9gag

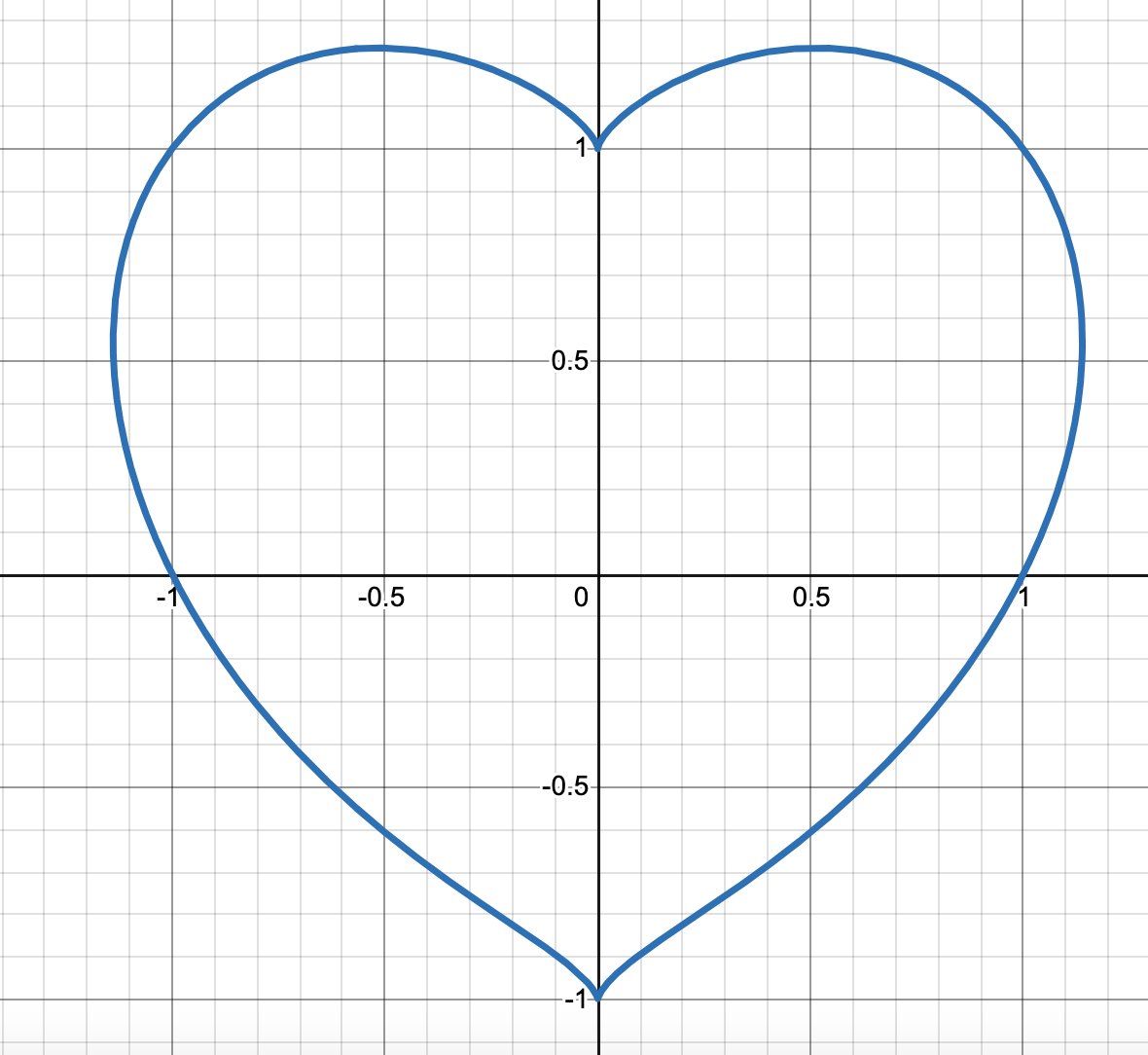
تويتر Chris Heilmann على تويتر X 2 Y 2 1 3 X 2y 3 T Co G0exoahf5v

Values Of A Bifar By 3 2 5x 2y 3 0 Represents A Circle Also Find The Radius An Centre Of The Circle

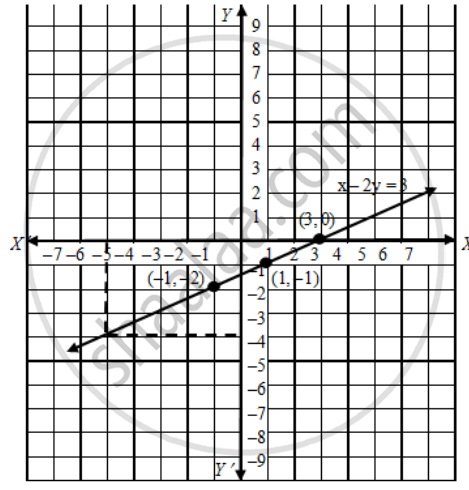
Draw A Graph Of The Line X 2y 3 From The Graph Find The Coordinates Of The Point When I X 5 Ii Y 0 Mathematics Shaalaa Com

Heart Pattern Background Clipart Text Line Font Transparent Clip Art

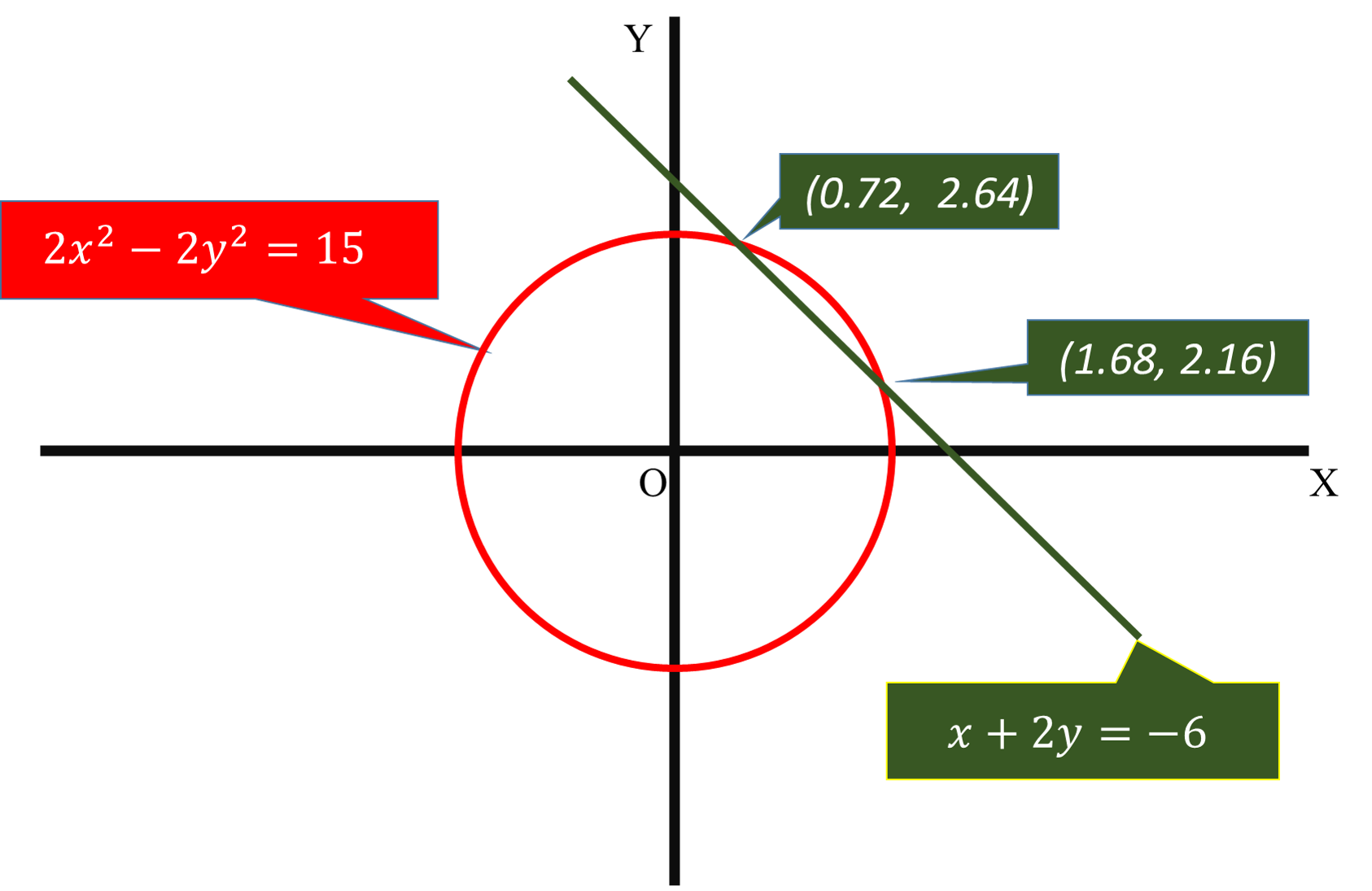
How Do You Solve The System 2x 2 2y 2 15 And X 2y 6 Socratic

Solved Review Problems In Problems 1 30 Solve The Equation Chegg Com

Y 3x 2 Y 0 X 1 X 2 Kasrusso

Find The Area Of The Triangle Formed By The Lines X 2y 3 0 3x 2y 7 0 And Y 1 0 Snapsolve

Solve 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 1 5 3x 2y 61 60 Mathematics Topperlearning Com 56o23roo

Solved Using Bernoulli Equation Solve The Differential Equation Given The Standard Form Dy Dx P X Y Y N Q X Course Hero

Solved Consider The Equation X 2y 3 X 1 Chegg Com

Solve Each Other Pair Of Equation Given Below Using Elimination Method 2y 3 X 12 5y 7 X 1 Mathematics Topperlearning Com D2p1cokk

Solve X Y 1 Dx 2x 2y 3 Dy 0 Youtube

All I Need Is X2 Y2 1 3 X2y3 0 I Love Mathematics Facebook

Solve X Y 2 Dx X 2y 3 Dy 0 Maths Differential Equations Meritnation Com

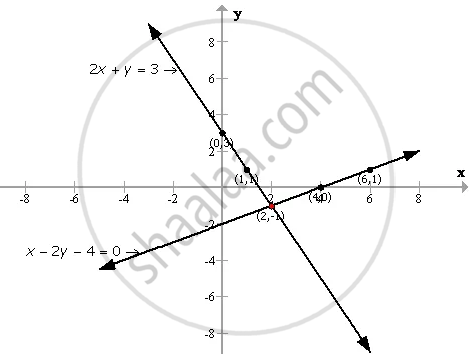
Solve Graphically The Simultaneous Equations Given Below Take The Scale As 2 Cm 1 Unit On Both The Axes X 2y 4 0 2x Y 3 Mathematics Shaalaa Com

Ex 6 3 12 Solve Graphically X 2y 3 3x 4y 12

The Line 2y X 3 Meets The Circle X 2 Y 2 2x 6y 15 0 At Points M And N Where N Is In The First Quadrant What Are The Coordinates Of M Andn Quora

Cbse 9 Math Cbse Linear Equations In Two Variables Ncert Solutions

1

If 2x 3y 2 3 4 0 And 3x 2y 2 2 1 5 Find X And Y Youtube

X 2y 1 Dx 2x 4y 3 Dy 0 X 2y U Youtube

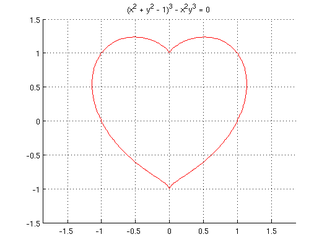
Trivia Captain V Twitter The Implicit Curve Equation X2 Y2 1 3 X2y3 0 Produces A Heart Shape When Graphed Nerdalert Http T Co F27je07r Twitter

Misc 9 Find Value Of P 3x Y 2 0 Px 2y 3 0

Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y

1

1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Respected Teachers Please Find The Value Of X And Y Mathematics Topperlearning Com 5qbsqgee

Maths Class 10if Frac 2x 3 Frac Y 2 Frac 1 6 0 And Frac X 2 Frac 2y 3 3 Then X Brainly In

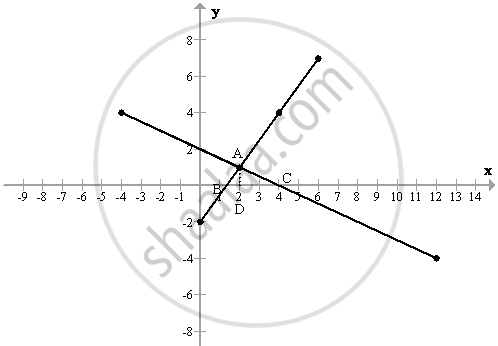
Solve Graphically The Following Equations X 2y 4 3x 2y 4 Take 2 Cm 1 Unit On Each Axis Also Find The Area Of The Triangle Formed

You Can Plot A Heart On A Graph I M A Nerd Heart Symbol Geek Stuff Happy Valentines Day

The Equation Of The Parabola Having Focus At 1 2 And The Directrix X 2y 3 0 Is Sarthaks Econnect Largest Online Education Community

Example 17 Line Perpendicular To X 2y 3 0 Passing

Math Mathematics Love X 2 Y 2 1 3 X 2y 3 0 Sacred Geometry Symbols Ornament Drawing Drawing Room Ceiling Design

X 2 Y 2 1 3 X 2 Y 3 0 Demotivation Us

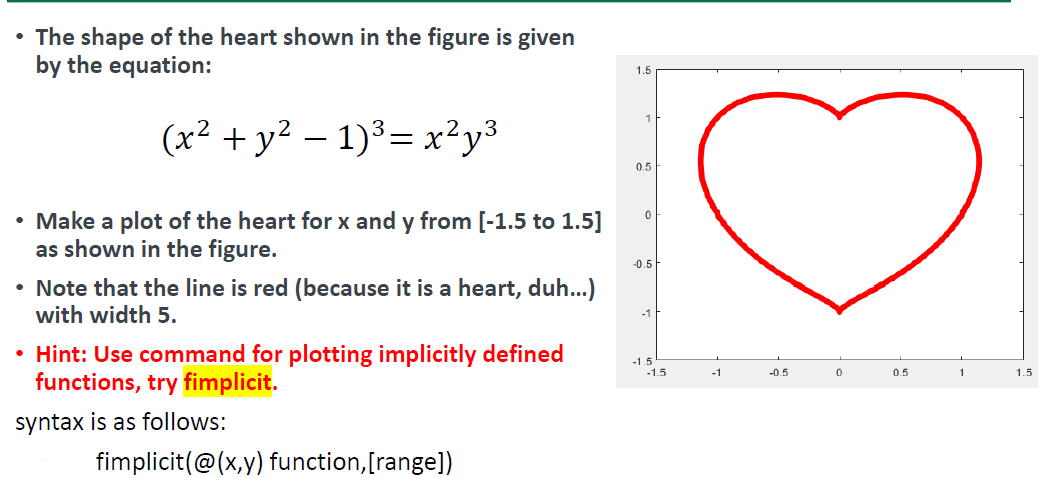
Solved The Shape Of The Heart Shown In The Figure Is Given Chegg Com

Amornivel Mi Amor Te Entrego Mi X 2 Y 2 1 3 X 2y 3 0 Ja140 Amormatematico Http T Co Cmwwg9ka5b Twitter

If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora

X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In

X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube

X 2 Y 2 1 3 X 2y 3 0 Wolfram Alpha Wolfram Mathematics Alpha

The Equation Of The Transvers And Conjugate Axes Of A Hyperbola Are Respectively X 2y 3 0 And 2x Y 4 0 And Their Respective Lengths Are Sqrt 2 And 2sqrt 3 Dot The Equation Of The Hyperbola Is 2 5 X 2y 3 2 3 5 2x Y 4 2 1

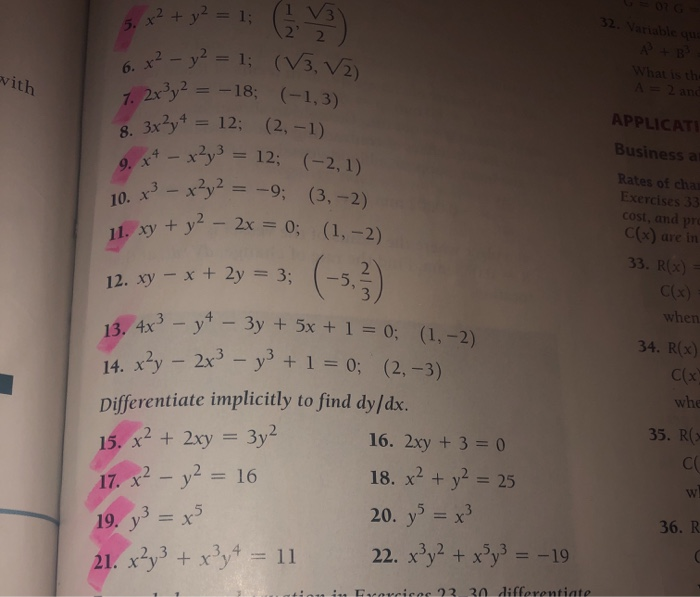
Solved 5 X Y 1 6 X2 Y2 1 V3 V2 8 3x Y 12 Chegg Com

1

1

Solve For X And Y X 2 2y 3 1 X Y 3 3 Sarthaks Econnect Largest Online Education Community

Solved Solve The Following Systems Of Equations By Cramer S Rule 1 X 2y 3 2 2x Y 3 3x Y 1 X Y 6 3 4a 2b 0 Sa

X 2y 3 2 And 2x Y 3 2 By Elimination Method Brainly In

Solved X 2 Y 2xy Y 3 0 X 0 Dy Dx X 2 Y 3 1 Chegg Com

Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection

The Radical Centre Of Three Circles X 2 Y 2 X 2y 3 0 X 2 Y 2 2x 4y 5 0 And X 2 Y 2 7x 8y 9 0 Is A 2 3 2 3 B 1 3 1 3 C 1 4 1 4 D 0 0

Solved On Matlab Please Do Part A And B Please Part A T

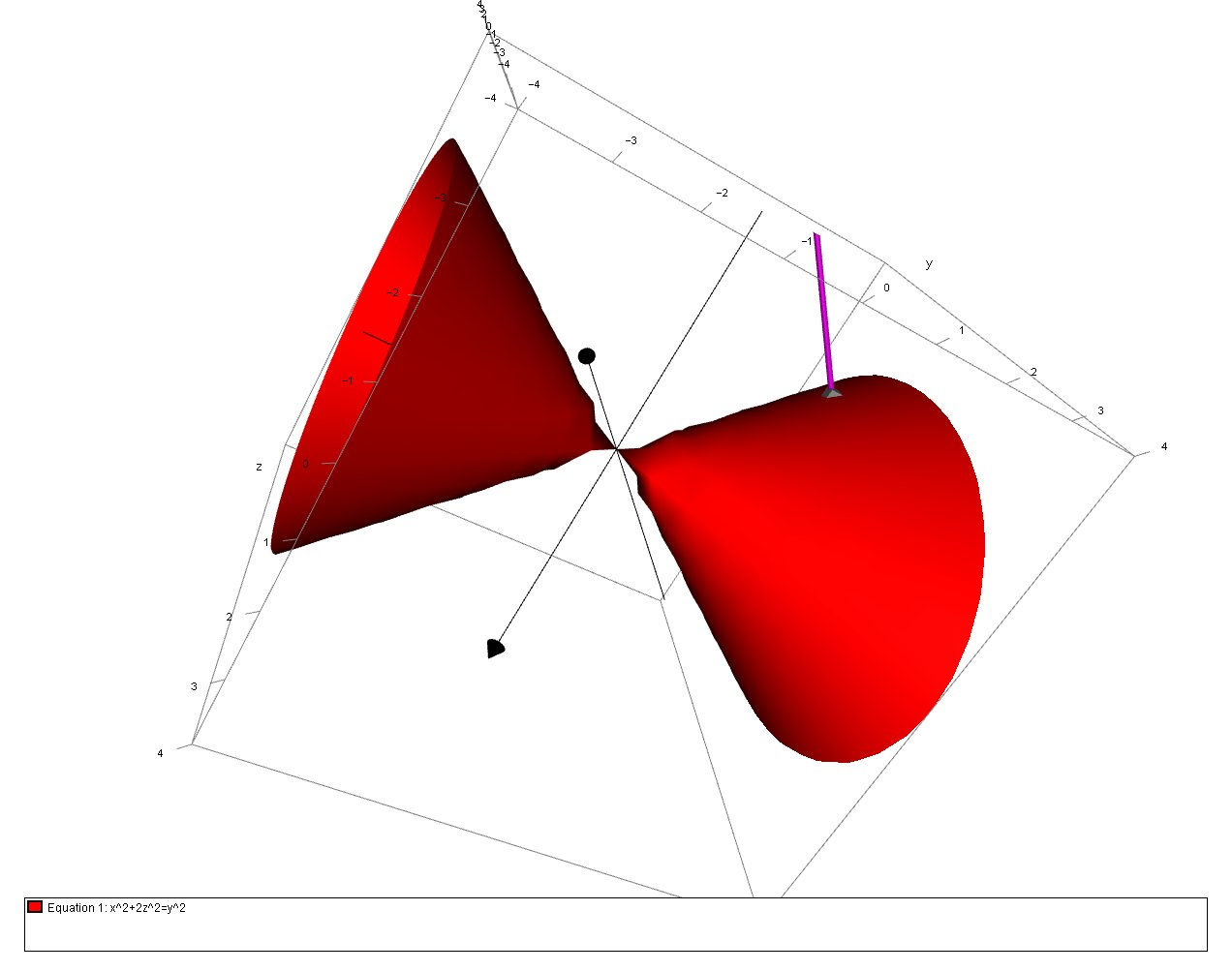
How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic

1 Jika X Dan Y Memenuhi Ftbeginarrayl 3 X 2 Gauthmath

Ex 6 3 14 Solve Graphically 3x 2y 150 X 4y 80

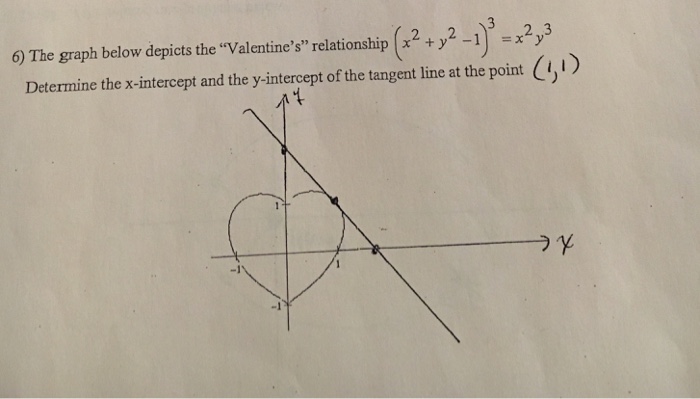
Solved 6 The Graph Below Depicts The Valentine S Chegg Com

Given The Four Lines With The Equations X 2y 3 0 3x 4y 7 0 2x 3y 4 0 4x 5y 6 0 Then Youtube

Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline

Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange

2x 4 3x 2 Y Y 2 2y 3 Y 4 0 Download Scientific Diagram

X 2 Y 2 1 3 X 2y 3 0 Hidekun Over Againのブログ 紅い と愛娘 みんカラ

Fil Heart Plot Svg Wikipedia

The Equation Of The Circle Having Its Centre On The Line X 2y 3 0 And Passing Through The Points Of Intersection Of The Circles X 2 Y 2

For Parabola X 2 Y 2 2x Y 6x 2y 3 0 The Focus Is Youtube